Ley de los cosenos
La ley de los cosenos es usada para encontrar las partes faltantes de un triángulo oblicuo (no rectángulo) cuando ya sea las medidas de dos lados y la medida del ángulo incluído son conocidas (LAL) o las longitudes de los tres lados (LLL) son conocidas. En cualquiera de estos casos, es imposible usar la ley de los senos porque no podemos establecer una proporción que pueda resolverse.La ley de los cosenos establece:
c 2 = a 2 + b 2 – 2 ab cos C .
Esto se parece al teorema de Pitágoras excepto que para el tercer término y si C es un ángulo recto el tercer término es igual 0 porque el coseno de 90° es 0 y se obtiene el teorema de Pitágoras. Así, el teorema de Pitágoras es un caso especial de la ley de los cosenos.
La ley de los cosenos también puede establecerse como
b 2 = a 2 + c 2 – 2 ac cos B or
a 2 = b 2 + c 2 – 2 bc cos A .
Ejemplos
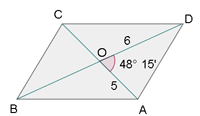
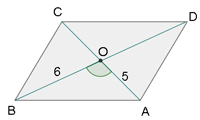
Las diagonales de un paralelogramo miden 10 cm y 12 cm, y el ángulo que forman es de 48° 15'. Calcular los lados.

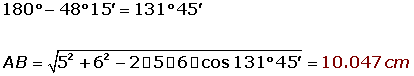
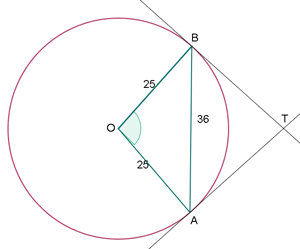
El radio de una
circunferencia mide 25 m. Calcula el ángulo que formarán las tangentes a
dicha circunferencia, trazadas por los extremos de una cuerda de
longitud 36 m.
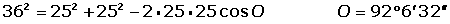

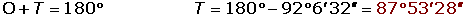




No hay comentarios:
Publicar un comentario